Na globalnom svjetskom nivou pandemija se i dalje širi velikom brzinom. Brzina i trend širenja virusa najviše odgovara matematičkom modelu eksponencijalne funkcije. Dakle svakim danom broj novih oboljelih (porast pozitivno testiranih pacijenata) je uvećan za broj oboljelih prethodnog dana multipliciran s eksponencijalnim faktorom.
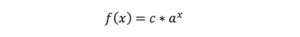
f(x) – broj pacijenata pozitivnih na corona na dan „x“
c – početni (referentni) broj pozitivnih npr. na dan 01. Mart 2020
x – vremenski period npr. 0,1,2,3,…(npr. Startni dan – pocetna mjera, prvi dan, drugi dan, treci dan, itd.)
a – exponecijalni faktor (npr. dvostruko vise, trostruko vise itd.)
Primjer exponencijalnog rasta
Ako stavimo na šahovska polja zrna riže tako da svako sljedeće šahovsko polje ima duplo više zrna riže od prethodnog (a = 2 u prethodnoj formuli) onda to izgleda ovako: prvo šahovsko polje (startno polje, x=0 u prethodnoj formuli) ima 1 zrno riže (c = 1 u prethodnoj formuli), drugo (x=1) 2 (a=2), treće (x=2) 4, četvrto 8, peto 16, šesto 32, sedmo 64, osmo 128, deveto 256, ….21. polje preko milion, itd. Zadnje, 64. šahovsko polje treba da ima 9 triliona zrna riže (9 i 18 nula), tj. računamo na 64-om polju ovako:

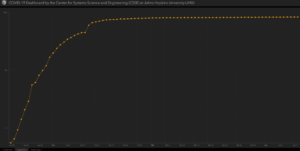
Primjenjujući ovu formulu na širenje virusa corone do sada, a koristeći bazu podataka iz zadnjih 14 dana koje prezentuje Johns Hopkins University, broj pozitivnih na COVID-19 se udvostručava svakih 7-12 dana.
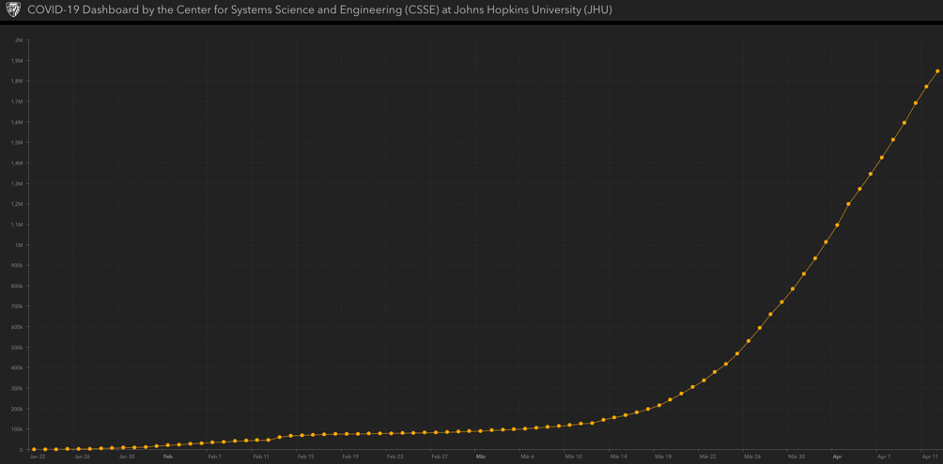
Ako je udvostručavanje u prosjeku svakih 11 dana, a što odgovara brojevima koje prezentira Johns Hopkins University, u tom slučaju broj pozitivnih na COVDI-19 računamo po danu npr. ovako:
Period udvostručavanja 11 dana rezultuje porastom po danu (exponencijalno):
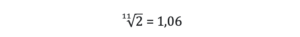
Prema tome matematički model širenja corone virusa na globalnom nivou izgleda ovako:
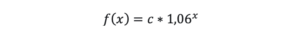
Ako je na dan x = 02.04.2020 bilo c=1 000 000 pozitivnih na COVID-19, po gornjoj formuli prognoza za 09.04.2020 ( nakon sedam dana) u svijetu pozitivnih na COVID-19 je:
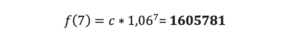
Stanje na stranici Johns Hopkins University na dan 09.04.2020 je 1600000.
Formula odstupa nešto oko 5700, a što je bilo i za očekivati, jer u ovoj jednostavnoj matematičkoj simulaciji nisu uzeti u obzir različiti faktori koji pospješuju ili usporavaju širenje pandemije.
Prognoza nakon 10 dana, dakle na dan 12.04.2020 bi izgledala ovako:
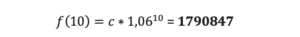
Stanje na stranici Johns Hopkins University na dan 12.04.2020 je 1800000.
Dakle odstupanje matematičke simulacije i realnih brojeva je u ovom slučaju manje od 1%.
Ova dva primjera potvrđuju da je formula (matematički model) prilično vjerodostojna i da može da bude korisna za planiranje, prognoziranje i preventivna djelovanja u svrhu smanjivanja intenziteta pandemije.
Iz gornjih primjera također vidimo da sa ovim trendom širenja COVIDA-19 jedan nosilac corona virusa, u prosjeku prenese za jedan dan na manje od dvije osobe (oko 1,06) corona virus.
Dakle 1 osoba može za manje od dva dana prenijeti virus na 2 druge osobe, tako da nakon 4 dana imamo između 6 – 8 novih pozitivnih pacijenata na COVID-19.
To je jedan od razloga što su mnoge zemlje uvele mjere svođenja socijalnih kontakata na minimum, a kako bi se pandemija usporila, kako bi se dobilo na vremenu i kako ne bi došlo do kolapsa zdravstva, a kako bi zdravstveni sistem bio u stanju pomoći onima sa teškim simptomima, drugim bolesnicima i naravno, kao najvažnije, da se maximalno umanji stopa smrtnosti.
Ali same mjere izolacije, distanciranja ili karantina mogu, ako budu neadekvatno i dugo primjenjivane, dovesti do dodatnih katastrofalnih posljedica.
Iz perspektive matematičkog modela strategija vračanja u „normalno življenje“ je postepena.
Prvi cilj je smanjivati exponencijalni faktor porasta novih pacijenata (u formuli faktor „a“) i pokušati dostići što manji porast novih pacijenata na dnevnoj bazi (porast od „0“ novih pozitivnih pacijenata bi bio ako je a=1). U tom slučaju formula bi izgledala ovako:
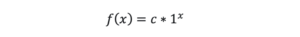
Drugi cilj je, već dosegnuti Prvi cilj (mali broj novih pozitivnih na corona virus), održati konstantno za „x“ vremena. U toj situaciji dolazi do prekretnice tj. nakon dostignutog maximuma corona pandemije mogući su sljedeći scenariji:
- Broj aktivnih nosilaca corona virusa je konstantan ili neznatno uvećan, jer broj izliječenih, umrlih i novih pacijenata održava ukupan broj pozitivnih pacijenata na podnošljivom nivou za zdravstveni sistem. Primjer takve „matematičke“ situacije je trenutno u Kini koja od početka marta javlja porast u prosjeku oko 100 novih pozitivnih slučajeva i ohrabrujuće brojeve onih koji su ozdravili.
broj aktivnih pacijenata = broj pozitivno testiranih – (broj umrlih + broj izliječenih)
Naravno, ovakva jednostrana interpretacija ne daje objektivnu sliku o pravom stanju u ovakvoj situaciji. Naime, koliki je intenzitet širenja virusa moguće je prepoznati samo ako se uzmu o obzir brojevi (porast) novih pacijenata pozitivnih na virus.
2. Broj aktivnih nosilaca corona virusa se smanjuje, jer je svakim danom sve veći broj onih koji su izliječeni (u toj konstelaciji je a<1 u matematičkom modelu). U takvoj situaciji govorili bi o smanjivanju tj. povlačenju pandemije.
3. Broj aktivnih nosilaca corona virusa se ne povećava, ali broj hitnih slučajeva i smrtnost je iznad nivoa koji može podnijeti jedan zdravstveni sistem. U takvoj situaciji region ili država se suočava ne samo sa COVID-19 pandemijom, nego i sa drugim problemima poput opasnosti od ekonomskog sloma i opasnosti da dođe i do drugih epidemija, prouzrokovanim neadekvatnim zbrinjavnjem bolesnih, siromašnih i bespomoćnih.
Specijalni slučajevi
U nekim regionima postoji uvjerenje da je „linearan“ rast porasta broja novih pozitivnih na corona virus dobar znak da poduzete mjere u borbi protiv corona pandemije pokazuju rezultate. Međutim realnost je potpuno drugačija. Linearan rast je samo prividno dobar znak, jer može u referentnom vremenskom intervalu prikazivati „ukupne brojeve“ manjim u odnosu na brojeve u nekom drugom okruženju. Naime jedini uspješan „matematički“ model je exponencijalni „trend“ širenja virusa „usporavati“ i takvim „usporavajućim“ trendom stvarati uslove za „zaustavljanje“ pandemije ili u idealnom slučaju okrenuti trend „exponencijalnog rasta“ u „exponencijalni pad“ (a<1). Naime linearna funkcija nema maximum, niti ima tangentu koja je dodiruje samo u jednoj mjernoj tački.
Sam linearan tok epidemije najvjerovatnije ukazuje na probleme u suzbijanju ili veoma često i na pogrešne statistike koje iz nekih razloga nisu realne. Na stranu što linearan tok bilo koje bakterijske, virusne ili radioaktivne „pandemije“ nije poznat.
Snaga pandemije
Sve do sada poznate epidemije i pandemije su završavale. Neke djelovanjem ljudi, cjepiva ili prirodnim putem stvaranjem kolektivnog imuniteta (imunitet krda), a neke su prestajale prirodnim putem. Ako posmatramo corona pandemiju kao “exploziju” atomske bombe tj. kao radioaktivnu reakciju, logično je očekivati da i sam virus corona nema neograničenu mogučnost multipliciranja i širenja. Dakle za očekivati je da se pandemija dostizanjem maximuma, a koji svijet do sada nije imao priliku da doživi, na neki način “istroši” ili “ugasi” i pandemija sama od sebe nestane.
Naravno najbolji scenario je da se što prije usavrši odgovarajuća vakcina. Ali kako stvari stoje to će trajati najmanje sljedečih 12 mjeseci. Na osnovu opisanog modela dolazi se do prognoze da bi nakon 12 mjeseci u svijetu bilo oko 2 milijarde pozitivnih na COVID-19, a broj umrlih bi bio zastrašujući, ako preslikamo današnju statistiku od 2% do 10%.
Trend širenja pandemije se ne razlikuje bitno u zemljama koje su uvele maximalne restriktivne mjere i u zemljama koje su odustale od drastičnih ogranićenja. Ta činjenica poteže potrebu analize i odgovora na pitanje
“Da li su sprovedene mjere samo prividno usporile pandemiju, jer mi tako interpretiramo uzroke i posljedice, ili bi pandemija i bez tih mjera imala istu snagu?”.
Sigurno je da nemamo iskustvene situacije iz prošlosti koje bi potkrijepile drugačije. Ipak potrebno je analizirati da li pandemija djeluje isto tj. ima isti trend rasta i kapaciteta sa ili bez restrikcija.
Jedina referenca koja potkrepljuje uvođenje socijalne restrikcije i “standbya” ekonomije je razvoj pandemije i poduzetih mjera u Kini tj. rezultati mjera u Kini, a koje svijet interpretira onako kako su prezentovani i od vodećih svjetskih institucija interpretirani.
Međutim brojevi koje zadnjih mjesec dolaze iz Kine, a koji svakodnevno izgledaju isti (u prosjeku 100 novih pozitivnih pacijenata po danu) stvaraju potrebu detaljnijeg interpretiranja i analize “kontrole pandemije”.
Gledajući iz perpektive (ne)poduzetih restriktivnih mjera u boljem položaju su zemlje koje nisu uvele restriktivne mjere, jer ogromni materijalni, tehnički i ljudski resursi koji su angažovani na suzbijanju pandemije i provođenju restriktivnih mjera, ostali su slobodni, a ekonomija tih zemalja nije pretrpjela gubitke, poput drugih.
Naravno, protiv pandemije je potrebno uvesti preventivne i druge mjere, ali je veoma bitno u pravom momentu prepoznati dugoročne prednosti ili konsekvence koje mogu nastupiti. Drugim riječima, kvalitativna analiza rizika mora uzeti u obzir i kvantitativni spektar poduzetih mjera, preventiva i restrikcija.
Dipl.-Ing. Hari Maslic (Business Analyst)